Generative Art with Compositional Pattern Producing Networks and GANs

*Note: This blog post accompanies code here, which has files for both the vanilla CPPN implementation and (broken) CPPN-GAN, and the new WGAN implementation. You can find the files for this post in the CPPN-GAN-OLD folder. A second attempt with Wasserstein GANs finds convergence. See further experiments in the follow up post!

How does one generate abstract art with software? One approach are genetic art programs, a type of algorithmic art generated using mathematical procedures (e.g. fractals). In this project I explore a type of genetic algorithm called Compositional Pattern Producing Networks. Furthermore, I attempt to (unsuccessfully) replicate Google Brain researcher David Ha’s experiments combining a Generative Adversarial Network with a CPPN architecture in the generator.

Compositional Pattern Producing Networks

CPPNs were devised by CS Professor Kenneth Stanley, as a way to prove that CPPNs were a legitimate abstraction of natural development encoding. While the above blog post describes CPPNs in greater detail, essentially as an genetic art tool, CPPNs generate abstract art by applying a function to generate each individual pixel in the image.

To generate an abstract image of size \(L * W\) pixels, for each pixel \([i, j], i \in 1...L, j \in 1...W\), let \(f(L_i, W_j) = s_{i, j}, s \in [0, 1]\), where \(s_{i, j}\) is the pixel intensity of pixel \([i, j]\) (for example, in greyscale, where 0 is total absence black and 1 is total presence white).

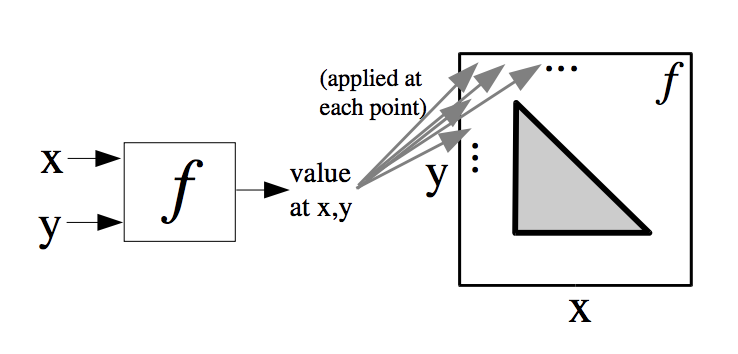
CPPN Diagram

In practice, we can use a feedforward neural net as f(), and add a few additional parameters to the function.

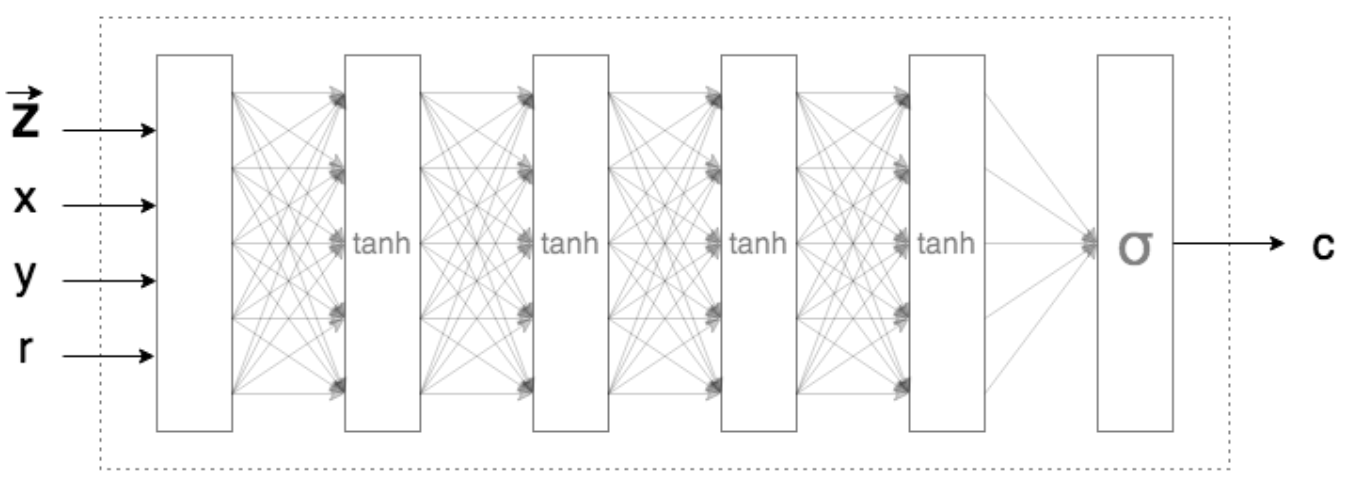
Let CPPN function be \(f(x_i, y_j, r, W, Z) = s_{i, j}\). Where:

The neural net architecture is up to the user’s choice but I opted for:

CPPN Architecture

Just by simply initializing the weights and running the feedforward net on each pixel, the model already produces interesting images. Furthermore, CPPNs work with input coordinates of any size, and holding all parameters and hyperparameters constant, a CPPN can generate an image with infinite resolution, depending on the size of the inputs!

The neural net can also be designed to output three values, for RGB color.

Combining the CPPN with a Generative Adversarial Network

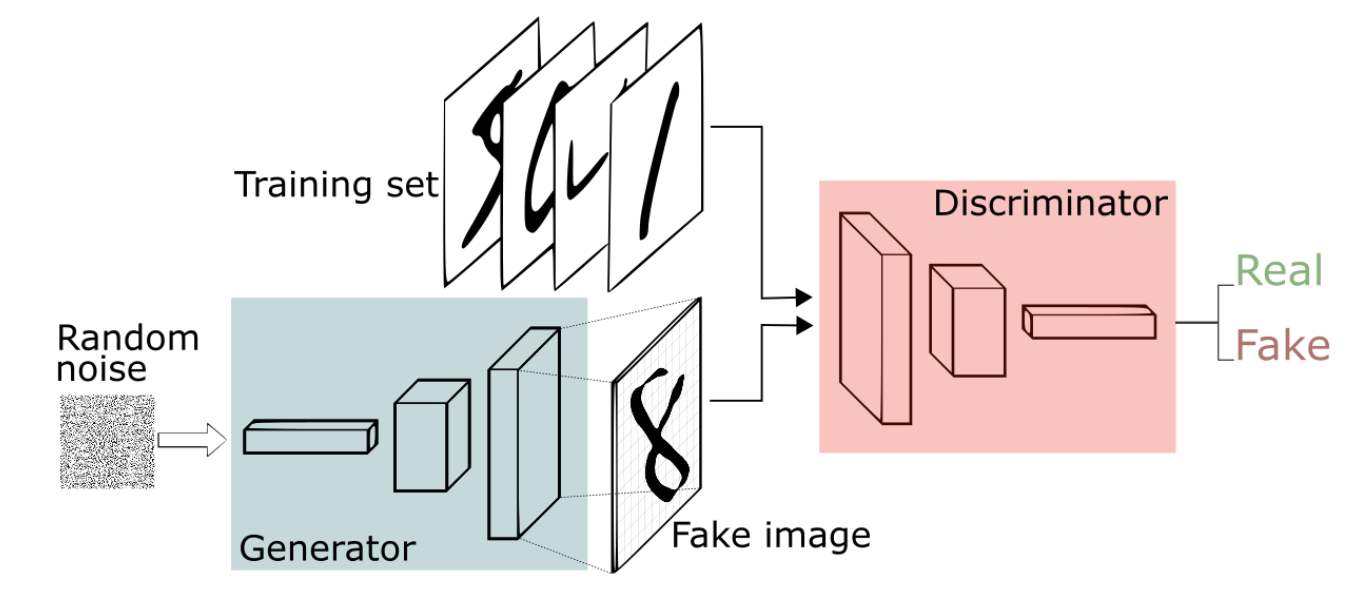
While CPPNs are interesting, the model has little control over the substantive design it creates. GANs on the other hand, attempt to generate new samples of data, from a preexisting dataset. Usually, image generating GANs are referred to as a type of DCGAN (Deep Convolutional), and utilize CNNs in both the discriminator and generator.

Here, in order to gain the “super-resolution power” of the CPPN, and the generative powers of a GAN, one can combine both models, by replacing the generator CNN architecture with the modified feedforward structure of a CPPN. Ideally, the GAN will be able to generate fake, but realistic images of the input dataset, and be capable of taking the generated samples to infinite resolution.

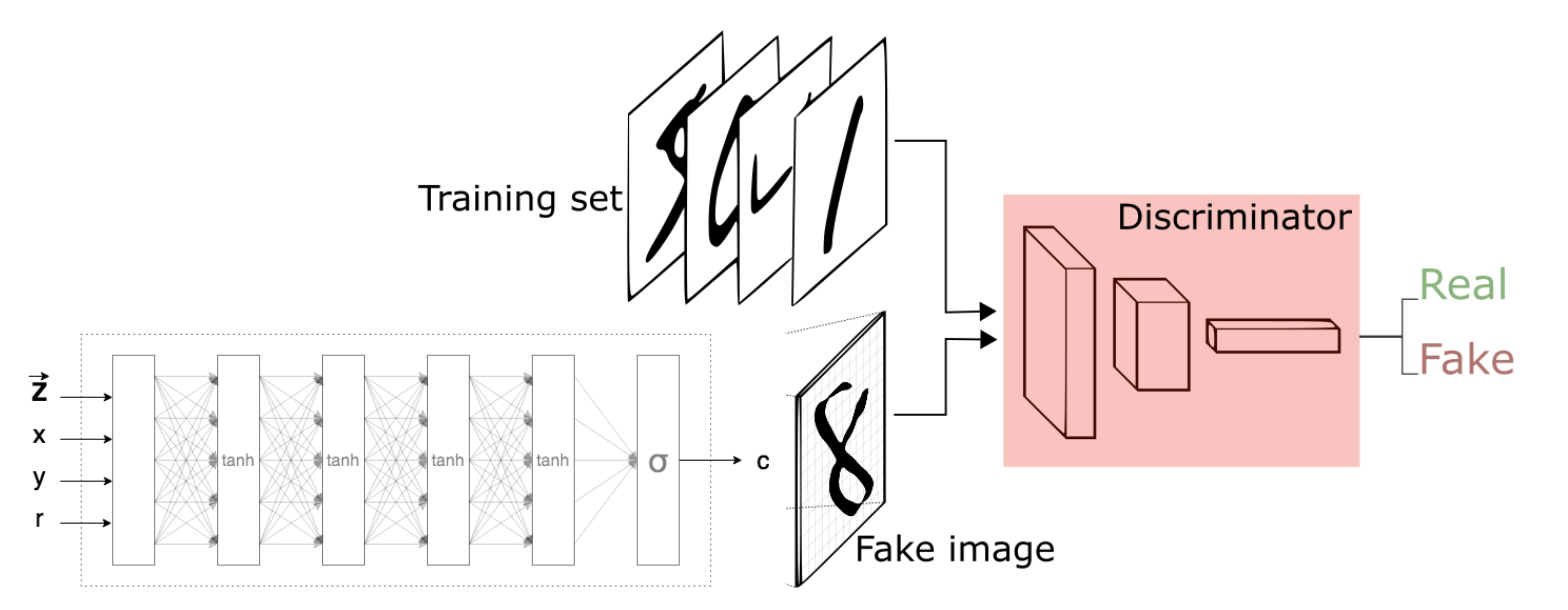
I attempted to use the MNIST dataset, but unfortunately, I was unable to get the GAN to train, and the samples turned out to be gibberish.

Nonetheless, upsampling some generated images yields interesting designs.

Lastly, like any other GAN model, one can still draw multiple samples from the latent \(Z\) space and interpolate one \(Z\) into another (i.e. slowly change the vector values, outputting/decompressing the image at every step).

Future work

Cool designs were generated but the ultimate goal here would be to get the model to actually train correctly. GANs are notorious for being hyperparameter sensitive and its unclear where I’ve gone wrong. Perhaps I can attempt to try Goodfellow’s improved techniques on GAN training, like minibatch discrimination, to fight mode collapse. Furthermore, it would be interesting to see this experiment done on other datasets, perhaps in color, using other GAN architectures.

References: